Unit 3: Introduction to heat transfer
In the following, we give you a short overview of thermal conductivity which is needed to understand why we need heating of homes (in a cold climate). What kind of physical processes are taking place? What kind of physical quantities are essential for in-room heating?
We need to heat our rooms when the outside air temperature is lower, or even, significantly lower than the recommended temperature. It is clear that there exists a heat transfer from the room to the outside through the walls and ceiling. The heat transfer is going in the opposite direction if the outside air temperature is higher than room temperature. Such kind of heat transfer takes place due to thermal conductivity.
Conduction heat transfer i.e. thermal conduction takes place without bulk motion of the matter.
Thermal conduction occurs in solid matter, liquids as well as in gases. The only factor for this is the temperature difference in the different parts of the system. Redistribution of the kinetic energy of the particles takes place due to collisions of the molecules in the gases or liquids, or propagation of oscillations through the solid bodies until the temperature in different parts of the system equals.
Thermal conduction can be characterized quantitatively by heat flux density which is defined as an amount of heat that flows through a unit area per unit time. As we know, the amount of heat per unit time is power. Thus the thermal conduction characterized by power flowing through the (wall) material determines the amount of heat needed for heating the rooms.
Exercise 3.1
To make sure you understood this explanation correctly, one small control question.
Now you should have some idea of what thermal conductivity is, and what kind of physical quantities can characterize it. Thermal conductivity is quantitatively characterized by the amount of heat Q going through the material. In Fig. 3.1 a cuboid is shown. This cuboid can be imagined as a piece of wall with thickness d and surface area S. As this amount of heat flows through the material, it is often called heat flux. The heat flux per unit time flowing per unit area is called heat flux density (or sometimes just heat flux) q.
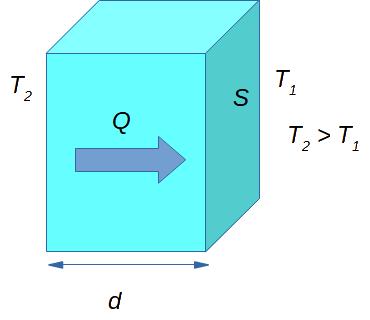
If we talk about the heat flux through the wall of a house (or other certain material), we can use the following formula to calculate the heat flux density q:
[latex]q = (K * S * \Delta T) / d[/latex]
(1)
where K (1 W/(m×K)) denotes the material thermal conductivity (coefficient), S (1 m2) is the area of the wall, ΔT (1 K) is the difference of temperatures on the different sides of the wall, and d (1 m) is the thickness of the wall. As we can see from Eq. (1) the heat flux density is given by watts. Thus, indeed, the heat flux density characterizes the power flow through the wall.
Note: Thermal conductivity means the physical phenomena characterizing heat transfer, but often this also means the thermal conductivity coefficient that characterizes the thermal properties of the material.
Exercise 3.2
Let us study the relation between heat flux density q and thermal conductivity K. Choose the correct statement.
Exercise 3.3
Now you should know, which is the relationship between the heat flux density q and thermal conductivity coefficient K of the wall material. Choose two wrong statements.
By our everyday experience we can say that a stone conducts heat better than a wood. It means that the heat flux through the stone is greater than through the wood, if other conditions remain the same (see Fig. 3.2).
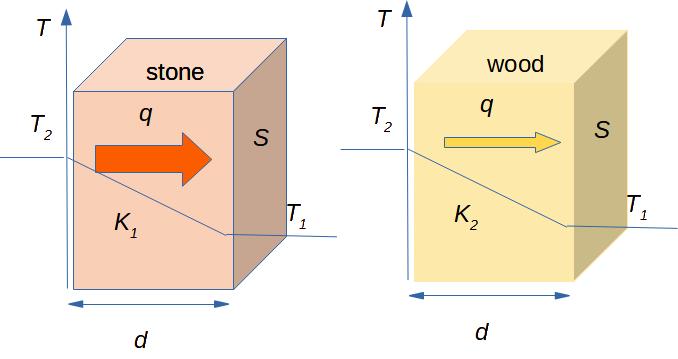
Use the following simulation to estimate how many times the thermal conductivities of stone, wood and metal differ.
You can check your conclusions by Table 3.2.
Table 3.2. Thermal conductivities of selected materials.
| Material | Thermal conductivity coefficient K (W/(K∙m)) |
| Brick | 0.84 |
| Wood | 0.16 |
| Glass | 0.94 |
| Rock wool | 0.033 |
| Concrete | 1.4-2.5 |
| Gyps sheet | 0.22 |
| Copper | 384 |
Exercise 3.4
Try to estimate the difference of heat fluxes through the brick wall and wooden wall. Choose two correct statements.
In order to estimate quantitatively how the change of wall material or thickness of material changes the heat flux (density) through the walls, we can use the program Desmos, where the Eq. (1) is entered.
Problem 3.1
For discussion: Let us suppose that you have a heating material (or just energy, in general) for 30 days. For how many extra days you have heating material if the temperature difference between inner and outer temperatures is decreased from 20°C to 18°C? From 10°C to 8°C?
