33 Silmaring: Rekursioon
Reeglina rekursiooni algkursusel ei käsitleta, siingi on see silmaringi materjalide hulgas. Kuna tegemist on niivõrd kena ja põneva teemaga, siis ei sobi jätta huvilisi nendest teadmistest ilma. Ei maksa nukrutseda, kui mingid kohad selles osas liiga keerulised tunduvad. Jäta need julgesti vahele!
Rekursioon
Tegelikult saab funktsiooni välja kutsuda ka selle sama funktsiooni sisemuses. Esialgu võib see tunduda võõras – kuidas siis saab nii olla, et me justkui õpetaksime mingit uut asja tegema sellesama asja abil, mida praegu õpetame?! Tegemist on rekursiooniga – arvutiteaduse ühe alusmõistega.
Rekursioon sobib eriti hästi selliste ülesannete lahendamiseks, kus tervikülesanne koosneb mingis mõttes sarnastest, kuid väiksematest alamülesannetest. Kui põhiülesannet piisavalt kaua alamülesanneteks jagades muutuvad alamülesanded nii väikeseks, et väiksemaks minna enam ei saa või ei taha, siis võiks püüda seda protsessi rekursiivselt esitada.
Faktoriaal
Klassikaline rekursiooni näide on faktoriaali arvutamine. Positiivse täisarvu n faktoriaal (tähistus n!) on n esimese positiivse täisarvu korrutis. Näiteks 4! = 1 · 2 · 3 · 4 = 24. Eraldi on kokku lepitud, et 0! = 1. Muidugi ka 1! = 1. Rekursiivsena saab faktoriaali leidmist kirjeldada nii, et iga järgmise arvu faktoriaali saame esitada eelmise arvu faktoriaali abil. Näiteks 4! = 4 · 3! ja omakorda 3! = 3 · 2! ning 2! = 2 · 1!. Üldistatult saame kaks haru:
- n! = 1, kui n = 0
- n! = n · (n-1)!, kui n > 0
Faktoriaali leidmise programm oleks selline:
Näiteprogramm. Faktoriaal
def faktoriaal(n):
if n == 0: # Rekursiooni baas
return 1
else: # Rekursiooni samm
return n * faktoriaal(n-1)
print(faktoriaal(4))
print(faktoriaal(0))
print(faktoriaal(400))
Rekursiivsetes programmides on alati mitu haru. Selleks, et protsess üldse kunagi lõppeks, peab vähemalt üks haru olema ilma rekursiivse väljakutseta. Seda haru nimetatakse rekursiooni baasiks. Rekursiivse väljakutsega (st sellesama funktsiooni väljakutsumisega) haru nimetatakse rekursiooni sammuks.
Rekursiooniga on seotud mitmed elulised teemad, näiteks küülikute paljunemise modelleerimine Fibonacci arvude abil jpm. Meie läheme aga visuaalsemate teemade juurde – hakkame vaatlema puid.
Korrapärane puu
Olgu meie eesmärgiks saada selline puu:
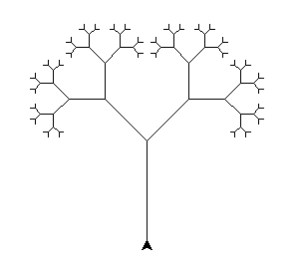
Terasel vaatlemisel märkame, et puu iga haru on ise omakorda samasugune puu, aga väiksem. Tolle väiksema puu iga haru on jällegi veel väiksem puu. Selliseid kujundeid, kus osa on terviku sarnane, nimetatakse fraktaliteks.
Teoreetiliselt võime lõpmatult joonistada puule väiksemaid oksi, aga praktiliselt poleks sel mõtet ja piiri seadmiseks võtame appi rekursiooni baasi. Näiteprogrammis jõuame rekursiooni baasini, kui järjekordse puu “tüve” pikkus on väiksem kui 5. Sellisel juhul joonistamegi ainult tüve, milleks liigume vastava arvu samme edasi ja seejärel kohe tagasi.
Rekursiooni sammu puhul aga joonistame tüve ja kaks haru, mis on omakorda ka puud, aga väiksemad (korrutame teguriga 0,6). Harude joonistamise eel, vahel ja järel tuleb kilpkonna ka sobivalt pöörata.
Käivita see programm. Näed ka, kui kaua kilpkonnal see joonistamine aega võtab. Selleks, et joonis kiiremini tekiks, võib kasutada funktsioone delay(0)speed(10).
Näiteprogramm. Rekursiivne puu
from turtle import *
def puu(pikkus):
if pikkus < 5: # Rekursiooni baas
forward(pikkus) # Ainult tüvi
back(pikkus)
else: # Rekursiooni samm
forward(pikkus) # Tüvi
left(45)
puu(0.6 * pikkus) # Haru, mis on väiksem puu
right(90)
puu(0.6 * pikkus) # Teine haru, mis on ka väiksem puu
left(45)
back(pikkus) # Tüvepidi tagasi
delay(0)
speed(10)
left(90)
puu(100)
exitonclick()
Loobume sümmeetriast
Eelmine puu oli meil väga korrapärane ja sümmeetriline. Loobume sellest, et puu peaks sümmeetriline olema. Muudame programmi nii, et enam ei pöörataks 45 kraadi vasakule, 90 paremale ja 45 vasakule. Olgu näiteks vasakule pöörded 40 ja 50 kraadi.
Näiteprogramm. Asümmeetriline puu
from turtle import *
def puu(pikkus):
if pikkus < 5:
forward(pikkus)
back(pikkus)
else:
forward(pikkus)
left(40) # Pöörame nüüd hoopis 40 kraadi
puu(0.6 * pikkus)
right(90)
puu(0.6 * pikkus)
left(50) # ja siin 50 kraadi
back(pikkus)
delay(0)
speed(10)
left(90)
puu(100)
exitonclick()
Näeme, et puu on tõesti natuke ebasümmeetriline:
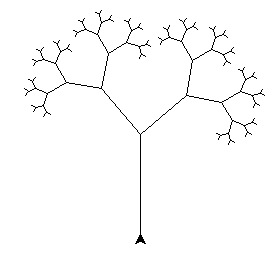
Päris puudel muidugi kõik harud ühepikkused pole. Proovime teha nii, et ühes harus oleks tegur endiselt 0,6 aga teisel hoopis 0,5.
Näiteprogramm. Erineva harupikkustega puu
from turtle import *
def puu(pikkus):
if pikkus < 5:
forward(pikkus)
back(pikkus)
else:
forward(pikkus)
left(40)
puu(0.6 * pikkus) # Tegur endiselt 0.6
right(90)
puu(0.5 * pikkus) # Tegur on nüüd 0.5
left(50)
back(pikkus)
delay(0)
speed(10)
left(90)
puu(100)
exitonclick()
Saame midagi sellist:
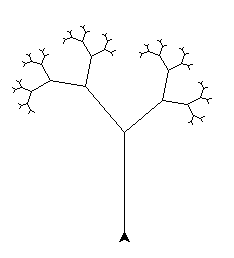
Juhuslik puu
Väga põnevaid võimalusi annab juhuslike arvude kasutamine. Nii annab sama programm igal käivitamisel erinevaid tulemusi. Muudame programmi nii, et iga haru joonistamisel määratakse tegur, millega pikkus korrutatakse, juhuslikult. Funktsiooniga randint(6,7)
Näiteprogramm. Juhusliku harupikkusega puu
from turtle import *
from random import * # Juhuslike arvude moodul
def puu(pikkus):
if pikkus < 5:
forward(pikkus)
back(pikkus)
else:
forward(pikkus)
left(40)
puu(randint(6,7) / 10 * pikkus) # Tegur on 0.6 või 0.7
right(90)
puu(randint(6,7) / 10 * pikkus) # Tegur on 0.6 või 0.7
left(50)
back(pikkus)
delay(0)
speed(10)
left(90)
puu(100)
exitonclick()
Tulemus võib olla midagi sarnast:
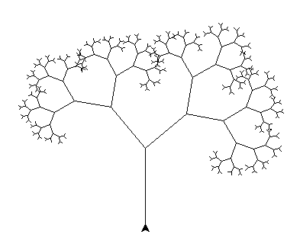
Teeme nüüd programmi, mis paneb mitu juhusliku suurusega puud kõrvuti.
Näiteprogramm. Juhuslike puude mets
from turtle import *
from random import *
def puu(pikkus):
if pikkus < 5:
forward(pikkus)
back(pikkus)
else:
forward(pikkus)
left(45)
puu(randint(6,7) / 10 * pikkus)
right(90)
puu(randint(6,7) / 10 * pikkus)
left(45)
back(pikkus)
def mets(puudearv):
i = 0
left(90)
while i < puudearv:
pendown()
puu(randint(20,59)) # Juhusliku pikkusega puu
penup()
right(90)
forward(randint(100,149)) # Puude vahe on ka juhuslik
left(90)
i = i + 1
delay(0)
speed(10)
mets(4)
exitonclick()
Antud juhul tekib nelja puuga mets:
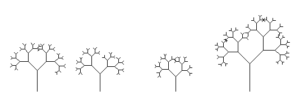
Korrast kaoseni
Kuigi me mitmeid asju muutsime ja lasime isegi juhuslikult arvutada, meenutasid saadud kujundid ikkagi puid. Teeme nüüd näiliselt suhteliselt väikese muudatuse, nimelt muudame ühe pööramise 45 kraadi asemel 44 kraadiks. Tõenäoliselt me silmaga nendel nurkadel vahet ei teeks.
Näiteprogramm. Kaootiline puu
from turtle import *
from random import *
def puu(pikkus):
if pikkus < 5:
forward(pikkus)
back(pikkus)
else:
forward(pikkus)
left(44)
puu(randint(6,7) / 10 * pikkus)
right(90)
puu(randint(6,7) / 10 * pikkus)
left(45)
back(pikkus)
delay(0)
speed(10)
left(90)
puu(100)
exitonclick()
Mis juhtub kujundiga?
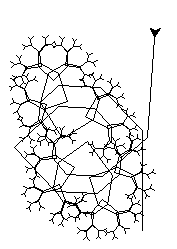
Näeme, et puuga enam tegemist pole ning et väike muudatus viis meid hoopis erineva kujundi juurde. Fraktalite puhul kipubki olema nii, et väike muudatus võib olla väga olulise tähendusega.

