98 Närvivõrgud ja PyTorch

Närvivõrkude alused

Närvivõrgud on tehisintellekti valdkonnas üks olulisemaid teemasid. Nad on võimelised õppima automaatselt ja avastama andmetes mustreid, mida inimestel käsitsi mõista ja programmeerida oleks olnud võimatu.

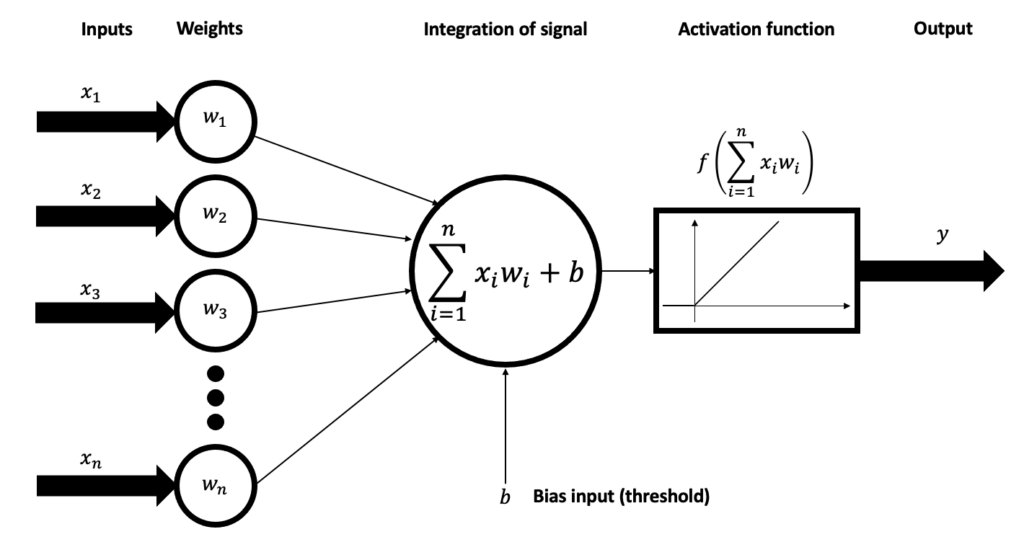
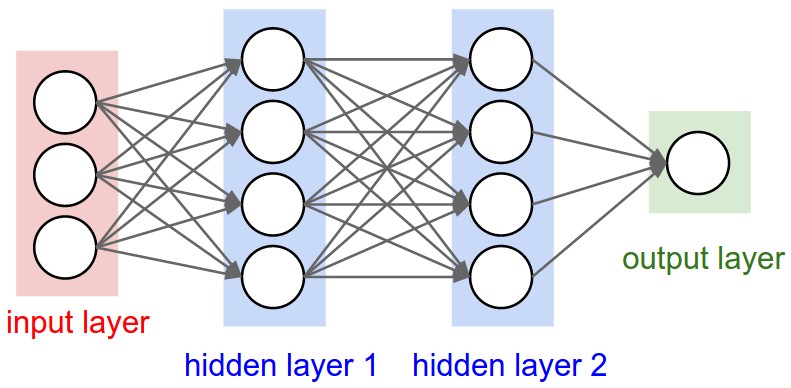
Närvivõrgud koosnevad erinevatest kihtidest. Kõige esimene kiht on sisendkiht, kuhu antakse sisendandmed. Näiteks kui sisendiks on mustvalge pilt, siis igaüks sisendkihi neuronitest vastab ühe piksli väärtusele (madal arv on must, kõrge arv on valge, vahepeal on hallid). Juhul kui pilt on värviline, siis sisendkihi neuronite arv on kolm korda suurem, kuna igaüks sisendkihi neuronitest vastab ühele RGB värvikanalile (punane, roheline ja sinine). Näiteks värviline pilt suurusega 32×32 pikslit vajaks 32 * 32 * 3 = 3072 pikslit. Sisendandmeteks võivad muidugi olla ka muud andmed, nagu tekst, heli, video, numbrid, jne.

Sisendile järgneb mingi arv peidetud kihte, mis samamoodi koosnevad neuronitest. Iga neuron on üks lineaarne funktsioon, mis tüüpiliselt võtab sisendiks kõik eelneva kihi neuronid ja annab väljundiks mingi väärtuse, mida jällegi edastatakse järgmisele kihile. Iga neuroni funktsioon näeb välja selline:

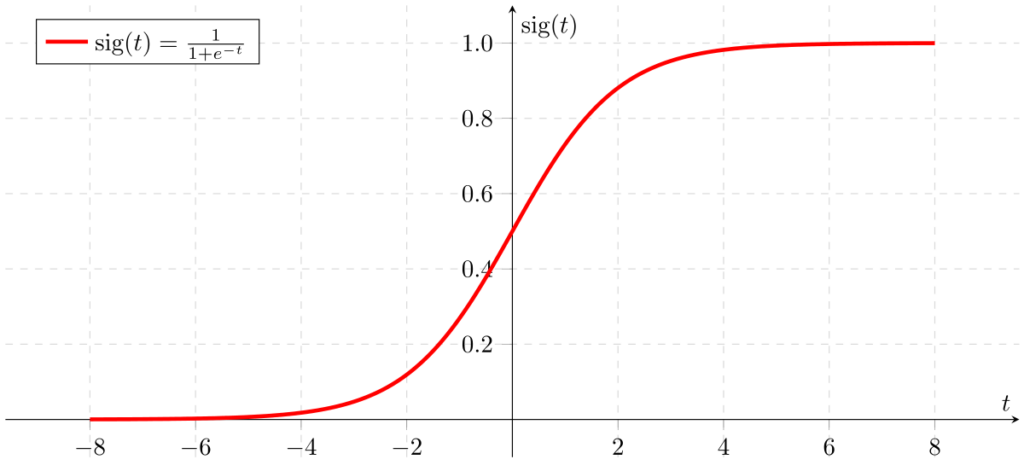
[latex]z[/latex] on neuroni väljundväärtus. [latex]x[/latex] on sisendandmete väärtused. [latex]w[/latex] on sisendandmetele vastavad kaalud, mis määravad, kui palju iga sisendneuroni väärtus mõjutab neuroni väljundväärtust. [latex]w[/latex] väärtused on tavaliselt algselt suvaliselt valitud ja millele leitakse algoritmiliselt optimaalsed väärtused alles närvivõrgu treenimise käigus. Lõpus on vabaliige [latex]b[/latex] (bias), mis alati nihutab neuroni väärtust mingi suuruse võrra. Kõiki närvivõrgu kaale koos kutsutakse ka närvivõrgu parameetriteks.

Tavaliselt rakendatakse neuronitele aktivatsioonifunktsiooni, mis transformeerib neuronite väljundväärtuseid mingiks uueks väärtuseks enne nende edasi saatmist.

Sümbol [latex]ϕ[/latex] tähistab aktivatsioonifunktsiooni. Väärtus [latex]a[/latex] on neuroni lõplik väljundväärtus, mis antakse edasi järgmise kihi neuronitele (või viimase kihi puhul antakse meile tagasi). Aktivatsioonifunktsioonid pole kohustuslikud, mispuhul [latex]a = z[/latex].

Küll aga on nad olulised, sest ilma nendeta pole võimalik lahendada mittelineaarseid probleeme.

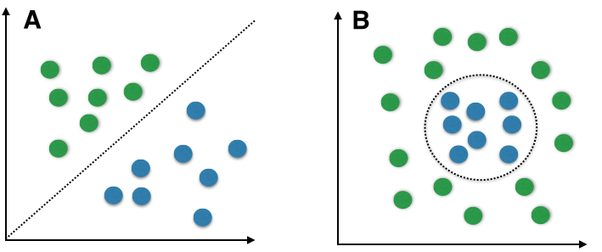
Sigmoidifunktsioon, mille väljundväärtused on 0-1 vahel, näeb välja selline:

Muutuja [latex]a[/latex] on lõplik neuroni väljundväärtus, mis antakse edasi järgneva kihi neuronitesse [latex]x[/latex]_{[latex]i[/latex]} kujul, kus [latex]i[/latex] on neuroni indeks kihis. Igal aktivatsioonifunktsioonil on oma eelised ja puudused. Näiteks ReLU aktivatsioonifunktsioon näeb välja selline:

ReLU funktsioon on kiirem kui sigmoidifunktsioon ta arvutuslihtsuse tõttu, kuid tal on ka mõningaid puudusi, nagu see, et ReLU funktsioon ei tagasta väärtusi (0, 1) piirkonnas, vaid [0,∞), mis võib olla mõnedes olukordades oluline.

Närvivõrgu viimast kihti kutsutakse väljundkihiks, mis sisaldab lõppandmetega neuroneid. Klassifitseerimisülesande väljundiks on klass, millesse antud sisend kuulub. Näiteks närvivõrk, mis tuvastab loomi, omaks ühte väljundneuronit iga looma kohta, mida ta on võimeline tuvastama. Kõige eredamat väljundneuronit (ehk neuronit, mille funktsioon tagastab suurima väljundi) loetaks närvivõrgu vastuseks.

Mõtle ja nuputa!

PyTorchi seadistamine

Kasutame närvivõrkude koostamiseks Pythoni raamistikku PyTorch, mida on võimalik alla laadida siit.

Kõiki näiteid võib proovida käima panna oma arvutis, mis eeldab, et vajalikud Pythoni pakid on installeeritud. PyTorch ise võtab vähemalt 3 GB kettaruumi. Osade näidete jooksutamine vajab arvutis head graafikakaarti või siis palju aega. Lokaalse installeerimise asemel on võimalus näiteid jooksutada näiteks Google Colab keskkonnas.

import torch

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)  # 'cpu' või 'cuda'

# loome tensoreid GPU-l või CPU-l
a = torch.tensor([1, 2, 3], device=device)
b = torch.rand(2, 2, 2, device=device)

Tensorid ja kihid

PyTorchi kasutamiseks tuleb importida torch moodul (kõikides järgnevates näidetes on see eeldatud). Tensor on PyTorchi peamine andmestruktuur, mis saab olla skalaar (arv), vektor (massiiv), maatriks (2D massiiv) või muu kõrgema-dimensiooniline struktuur. Praktikas sarnaneb ta mitmemõõtmeliste NumPy massiividega. Tensorite loomiseks on mitmeid võimalusi, millest paljud sarnanevad NumPy süntaksile. Näiteks:

import torch  # edaspidistes näidetes alati eeldame, et torch on imporditud!

a = torch.tensor([[1, 2], [3, 4]])  # loome 2D tensori läbi listi
print(a)
# tensor([[1, 2],
#         [3, 4]])

b = torch.rand(3, 4)  # nt siia võib lisada ka device=device
print(b)
# tensor([[0.5436, 0.6467, 0.9512, 0.6870],
#         [0.4695, 0.0687, 0.1261, 0.5235],
#         [0.7589, 0.3855, 0.2477, 0.0452]])

print(b.shape)         # torch.Size([3, 4])
print(b[0])            # tensor([0.5436, 0.6467, 0.9512, 0.6870])
print(b[0, 0])         # tensor(0.5436)
print(b[0, 0].item())  # 0.5436
print(b[:, -1])        # tensor([0.6870, 0.5235, 0.0452])

Tensoritel on olemas ka palju dimensioonidega seotud operatsioone (mis ei muuda tensoreid ise, vaid tagastavad uue tensori):

c = torch.zeros(4)
print(c)  # tensor([0.,  0.,  0.,  0.])

# lisame dimensiooni positsiooni 0
print(c.unsqueeze(0))  # tensor([[0.,  0.,  0.,  0.]])

# lisame dimensiooni positsiooni 1
print(c.unsqueeze(1))  # tensor([[0.], [0.], [0.], [0.]])

d = torch.tensor([[[[1], [2]], [[3], [4]]]])

# kustutame üleliigsed dimensioonid
print(d.squeeze())  # tensor([[1, 2], [3, 4]])

# teisendame tensori 1D massiiviks
print(d.flatten())  # tensor([1, 2, 3, 4])

Iga närvivõrgu peidetud kihi sisendiks ja väljundiks on tensor. Esimese peidetud kihi sisendiks saaks näiteks olla pilt, mille pikslid on esitatud vektorina. Väljundiks võiks olla näiteks 10-kohaline vektor, mille iga element vastab mingile pildikategooriale.

Koostame kihid närvivõrgule, mis ennustab koosinusfunktsiooni [latex]f(x) = cos(x)[/latex] väärtusi (mistõttu vajab ta vaid ühte sisendneuronit [latex]x[/latex] ja ühte väljundneuronit [latex]f(x)[/latex]ennustatud väärtusele):

from torch import nn

hidden_layer = nn.Linear(1, 7)  # 1 sisendneuron, 7 väljundneuronit
activation_fn = nn.ReLU()       # ReLU aktivatsioonifunktsioon
output_layer = nn.Linear(7, 1)  # 7 sisendneuronit peidetud kihist, 1 väljundneuron

x = torch.tensor([50.0])  # kihi sisendiks oodatakse alati listi
y = torch.cos(x)          # arvutame ette õige vastuse, mida AI peab ennustama
print(x, y)               # tensor([50.]) tensor([0.9650])

z = hidden_layer(x)   # z on 10-elemendine vektor
a = activation_fn(z)  # a on transformeeritud 10-elemendine vektor

print(z, '\n', a)
# tensor([29.3417, -37.906, -39.440, 21.4118, 21.6470, 17.2586, -2.5133])
# tensor([29.3417,  0.0000,  0.0000, 21.4118, 21.6470, 17.2586,  0.0000])

Nagu näeme, ReLU aktivatsioonifunktsioon [latex]a = max(z, 0)[/latex] muudab kõik negatiivsed väärtused nulliks. Muutuja a on nüüd meie järgmise kihi sisend, mis annab väljundiks ühe neuroni. See väljundneuron peaks peale treenimist oskama ennustada, et [latex]cos(50) = 0.9650[/latex].

Väljundneuronile me aktivatsioonifunktsiooni ei rakenda, sest me tegeleme regressiooniga (mingi väärtuste, mitte klassi, ennustamine).

y_hat = output_layer(a)  # närvivõrgu ennustus
print(y_hat)             # tensor([13.5124])
print(y)                 # tensor([0.9650])

Muutuja y_hat on meie ennustus, mille matemaatiline notatsioon on [latex]\hat{y}[/latex]. Kuna närvivõrku pole veel treenitud ja seetõttu ta ei tea mida teha, annab ta meile täielikult suvalise vastuse. Õnneks on PyTorchis treenimise matemaatiline pool suuresti automatiseeritud: me peame vaid ütlema närvivõrgule, kui vale ta ennustus on. Seejärel oskab närvivõrk ise ennast korrigeerida, et järgmine kord ta ennustus oleks täpsem.

Võime näiteks vaadata peidetud kihi parameetreid [latex]w[/latex] niiviisi:

print(hidden_layer.weight)
# tensor([[0.5847], [-0.7390], [-0.7715], [0.4361], [0.4337], [0.3365], [-0.0392]])

Kahjufunktsioonid

Et treenimist alustada, tuleb meil võtta näidisandmete komplekt [latex]x[/latex] ja [latex]y[/latex] ning alustuseks arvutada sellele ennustus [latex]\hat{y}[/latex], mida me eelmises peatükis juba ka tegime.

Järgmine samm on arvutada läbi [latex]y[/latex] ja [latex]\hat{y}[/latex] väärtuste välja kahju (loss). Selleks kasutame kahjufunktsiooni (loss function), mis leiab, kui suur on meie ennustuse ja tegeliku väärtuse vahe. Sellised kahjufunktsioone on palju, aga meile piisab populaarsest valikust MSE (mean squared error):

Siin jätkame eelmise peatüki näite lõpust:

loss_fn = nn.MSELoss()  # loome 'Mean Squared Error' funktsiooni
loss = loss_fn(y_hat, y)  # arvutame kahju: mida väiksem on tulemus, seda õigem on ennustus
print(loss)  # tensor(157.4369)

Tulemuse peal loss.backward() meetodi välja kutsumine leiab vajalikud muutused (ehk gradiendid) kihtide [latex]w[/latex] parameetritele, et tulevikus antud x-ile sarnase väärtuse korral teha parem ennustus. Parameetrite gradiendid salvestatakse tensorite .grad atribuuti.

loss.backward()  # leiame, kui palju peame muutma iga kihi parameetrit, et kahju oleks väiksem

# gradiendid näitavad, kui palju iga kaaluparameeter peaks muutuma
print(hidden_layer.weight.grad)  # tensor([[142.13], [0.], [0.], [241.06], [294.88], [69.76], [0.]])

Optimeerijad

Nüüd kui oleme leidnud gradiendid, peame koostama optimeerija, mis neid muudatusi ka tegelikult parameetritele rakendab. Selles näites kasutame lihtsat SGD (stochastic gradient descent) optimeerijat. Optimeerijale peame andma ka õpisammu (learning rate), mis määrab, kui kiiresti meie kihtide parameetrid muutuvad relatiivselt gradientide suurustele. Optimaalse õpisammu hüperparameetri lr väärtuse leiame läbi katsetamise, aga tavaliselt alustatakse väärtustega 0.1, 0.01 või 0.001. Liiga madal arv võib panna närvivõrgu õppima mõttetult aeglaselt, liiga kiire paneb aga parameetrid muutuma liiga kiirelt ja võib juhtuda, et närvivõrk ei õpigi üldse midagi.

Jätkame näidet:

# loome optimeerija, mis teeb muudatusi hidden_layer-i parameetrites vastavalt kahjufunktsiooni tulemustele
optimizer = torch.optim.SGD(hidden_layer.parameters(), lr=0.1)  # kasutame õpisammu 0.1

# vaatame uuesti algseid kaale ja gradiente
print(hidden_layer.weight)       # tensor([[0.584], [-0.739], [-0.771], [0.436], [0.433], [0.336], [-0.03]])
print(hidden_layer.weight.grad)  # tensor([[142.13], [0.], [0.], [241.06], [294.88], [69.76], [0.]])

optimizer.step()  # teeme muudatused

print(hidden_layer.weight)  # vaatame, kuidas kaalud muutusid
# tensor([[-13.6292], [-0.7390], [-0.7715], [-23.6709], [-29.0547], [-6.6397], [-0.0392]])

# juhul kui soovime uuesti muudatusi teha, peame alguses eelmised gradiendid nullima
# kui me seda ei teeks, sis järgmise iteratsiooni gradiendid oleksid liidetud juurde eelnevatele
optimizer.zero_grad()  # kustutame hidden_layer-i parameetrite gradiendid
print(hidden_layer.weight.grad)  # tensor([[0.], [0.], [0.], [0.], [0.], [0.], [0.]])

Lõpuks võime lasta närvivõrgul teha ennustuse uuesti sama x väärtusega:

z = hidden_layer(x)
a = activation_fn(z)
y_hat = output_layer(a)
loss = loss_fn(y_hat, y)

print(y_hat, y)  # tensor([0.0277]) tensor([0.9650])
print(loss)  # tensor(0.8784)

Näeme, et meie loss on muutunud väiksemaks, ehk meie ennustus on seekord täpsem. Eelmine kord ennustas närvivõrk [latex]\hat{y} = 13.5124[/latex], see kord aga [latex]\hat{y}= 0.0277[/latex]. Kuna õige vastus on [latex]y = 0.965[/latex], jõudsime õigele vastusele tunduvalt lähemale. Kuna närvivõrk oskab funktsioone ainult jäljendada, siis täpselt õige vastuseni me arvatavasti kunagi ei jõuagi. Lisaks sellele, praegune närvivõrk ikka veel annaks suvalisi vastusi paljude teiste x väärtuste puhul, sest me pole talle veel nende kohta näiteid andnud.

Lisainfo: Gradiendi laskumine (gradient descent)

Gradiendi laskumise algoritmi põhiolemus on see, et ta liigub kahjufunktsiooni kõrgematest kohtadest madalamatesse, kuni jõuab mingi piirini, kus muutusi enam ei toimu. Kalkuluse terminites, otsitakse kahjufunktsiooni lokaalset miinimumpunkti. Laskumiskiirus oleneb learning rate (LR) hüperparameetrist. Liiga kõrge laskumiskiirus tekitab olukorra, kus algoritm hakkab lendama optimaalsest madalaimast punktist mööda.

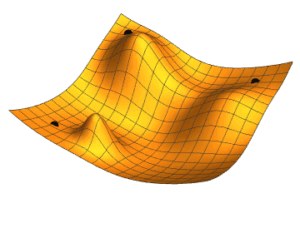
Kahjufunktsiooni maastikud on tegelikkuses hästi keerulised ja mitteühtlased, ning koosnevad tavaliselt tuhandetest või miljonitest dimensioonidest.