Meenutusi funktsioonist

Programmeerimises on äärmiselt tähtis uute alamprogrammide loomine. Tegelikult suuresti selles programmeerimine seisnebki. Pythonis nimetetakse alamprogramme funktsioonideks. Varasemas oleme funktsioone juba paljudes kohtades rakendanud ehk välja kutsunud. Kui funktsioon on defineeritud, aga seda pole veel rakendatud, siis on tegemist nagu ükskõik millise tarbeeseme või masinaga, mis on küll olemas, aga mida (veel) ei kasutata.

Eespool oleme funktsioone rakendanud n-ö põhiprogrammis, aga ka teiste funktsioonide kirjeldustes. Näiteks järgmises programmis on põhiprogrammis kaks korda rakendatud funktsiooni ruut. Funktsiooni ruut kirjelduses aga on kasutatud funktsioone forward ja left.

from turtle import *

def ruut(): # Defineerime funktsiooni nimega ruut
i = 0
while i < 4:
forward(100)
left(90)
i = i + 1

ruut() # Kutsume funktsiooni ruut välja. Kilpkonn joonistab ruudu küljega 100 pikslit
right(45) # Pöörame paremale 45°
ruut() # Kutsume uuesti funktsiooni ruut välja

exitonclick()

Rekursioon

Tegelikult saab funktsiooni välja kutsuda ka selle sama funktsiooni sisemuses. Esialgu võib see tunduda võõras – kuidas siis saab nii olla, et nagu õpetaksime mingit uut asja tegema sellesama asja abil, mida praegu õpetame?! Tegemist on rekursiooniga – arvutiteaduse ühe alusmõistega. Reeglina rekursiooni algkursusel ei käsitleta, siingi on see silmaringi materjalide hulgas. Kuna aga tegemist on niivõrd kena ja põneva teemaga, siis ei saa jätta ka selle kursuse huvilisi sellest ilma. Küll aga palun mitte nukrutseda, kui mingid kohad selles osas liiga keerulised tunduvad. Jätke need julgesti vahele! Nädala lõputestis siiski ühtteist on vaja teada.

Rekursioon sobib eriti hästi selliste ülesannete lahendamiseks, kus tervikülesanne koosneb mingis mõttes sarnastest, kuid väiksematest alamülesannetest. Kui põhiülesannet piisavalt kaua alamülesanneteks jagades muutuvad alamülesanded nii väikeseks, et väiksemaks enam minna ei saa või ei taha, siis võiks püüda seda protsessi rekursiivselt esitada.

Klassikaline rekursiooni näide on faktoriaali arvutamine. Positiivse täisarvu n faktoriaal (tähistus n!) on n esimese positiivse täisarvu korrutis. Näiteks 4! = 1 · 2 · 3 · 4 = 24. Eraldi on kokkulepitud, et 0! = 1. Muidugi ka 1! = 1. Rekursiivsena saab faktoriaali leidmist kirjeldada nii, et iga järgmise arvu faktoriaali saame esitada eelmise arvu faktoriaali abil. Näiteks 4! = 4 · 3! ja omakorda 3! = 3 · 2! ning 2! = 2 · 1!. No ja 1! = 1 või kui tahame 0 ka mängu võtta, siis võime öelda ka, et 1! = 1 · 0! ja 0! = 1. Üldistatult saame kaks haru:

• n! = 1, kui n = 0
• n! = n · (n-1)!, kui n > 0

Programm aga on siis selline.

def faktoriaal(n):
    if n == 0: # Rekursiooni baas
        return 1
    else: # Rekursiooni samm
        return n * faktoriaal(n-1)

print(faktoriaal(4))
print(faktoriaal(0))
print(faktoriaal(400))

Rekursiivsetes programmides ongi alati mitu haru. Selleks, et protsess üldse kunagi lõppeks, peab vähemalt üks haru olema ilma rekursiivse väljakutseta. Seda haru nimetatakse rekursiooni baasiks. Rekursiivse väljakutsega (st sellesama funktsiooni väljakutsumisega) haru nimetatakse rekursiooni sammuks.

Rekursiooniga on seotud mitmed elulised teemad, näiteks küülikute paljunemise modelleerimine Fibonacci arvude abil jpm. Meie läheme aga visuaalsemate teemade juurde – hakkame vaatlema puid.

Korrapärane puu

Olgu meie eesmärgiks saada selline puu.

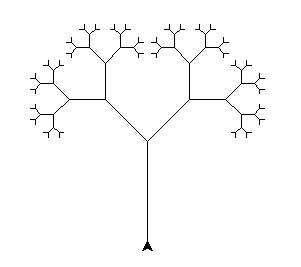
Natuke terasemal vaatlemisel märkame, et puu iga haru on ise ka omakorda samasugune puu, aga väiksem. Tolle väiksema puu iga haru on jällegi veel väiksem puu. Selliseid kujundeid, kus osa on terviku sarnane, nimetatakse fraktaliteks.

Teoreetiliselt võime lõpmatult joonistada puule väiksemaid oksi, aga praktiliselt poleks sel mõtet ja piiri seadmiseks võtame appi rekursiooni baasi. Näiteprogrammis jõuame rekursiooni baasini, kui järjekordse puu “tüve” pikkus on väiksem kui 5. Sellisel juhul joonistamegi ainult tüve, milleks liigume vastava arvu samme edasi ja kohe tagasi.

Rekursiooni sammu puhul aga joonistame tüve ja kaks haru, mis on omakorda ka puud, aga väiksemad (korrutame teguriga 0,6). Harude joonistamise eel, vahel ja järel tuleb kilpkonna ka sobivalt pöörata.

Palun pange see programm tööle, näete ka, kui kaua kilpkonnal see joonistamine aega võtab. Selleks, et joonis kiiremini tekiks, võib kasutada funktsioone delay(0) ja speed(10).

from turtle import *

def puu(pikkus): 
    if pikkus < 5: # Rekursiooni baas
        forward(pikkus) # Ainult tüvi
        back(pikkus)
    else: # Rekursiooni samm
        forward(pikkus) # Tüvi
        left(45)
        puu(0.6 * pikkus) # Haru, mis on väiksem puu
        right(90)
        puu(0.6 * pikkus) # Teine haru, mis on ka väiksem puu
        left(45)
        back(pikkus) # Tüvepidi tagasi

delay(0)
speed(10) 
left(90)
puu(100)

exitonclick()

Rohkem saad lugeda rekursioonist ja kilpkonnagraafikast:

https://courses.cs.ut.ee/2017/eprogalused/spring/Main/Silmaring-rekursioon